For scalable structured optimization, we have pushed the boundaries of running time and solution quality by (i) bridging discrete and continuous optimization, (ii) developing novel approximation methods, often multi-criteria, and (iii) exploiting submodularity and combinatorics of the solution space. This includes faster algorithms for structured convex optimization, new ways of rounding relaxed solutions, reusing information from previous subproblems in iterative methods, and improved the quality of solutions in terms of approximation factors. With the growing computational demands of our era, we are looking into new primitives in optimization and bringing machine learning within optimization subroutines for scaling to next-generation applications. We are one of the first research groups in the world to bring the concept of warm-starts in quantum optimization. We are currently exploring other classical techniques that can be used to speed up hybrid quantum algorithms, such as sparsification of problem instances, decomposition, warm-starts for other combinatorial problems, incorporation of constraints, etc.
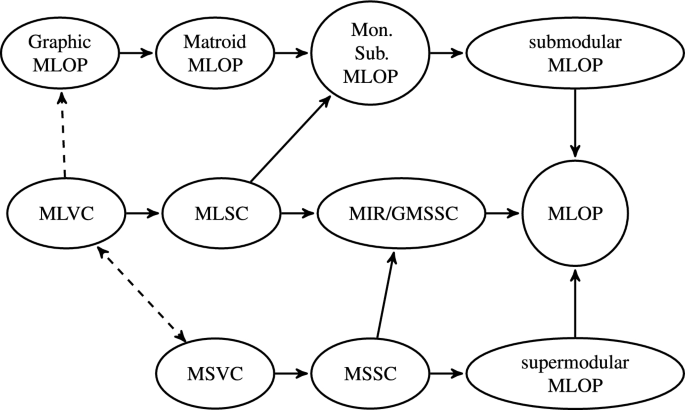
(a) Bridging Discrete and Continuous Optimization: There are significant gaps in our knowledge when it comes to convex optimization over combinatorial polytopoes, even though these polytopes arise frequently in many applications. This is simply due to the fact that the theory of discrete algorithms has evolved largely independently compared to general continuous optimization methods. We settled Bach’s conjecture by exploiting duality of convex minimization over submodular polyhedra (spotlight in NeurIPS), gave the first pyramidal width independent bound for Frank-Wolfe algorithms by analyzing descent directions for constrained optimization, and reduced the time for line search in submodular polyhedra by analyzing the discrete Newton method. We are rapidly developing the theory of combinatorial polytopes using continuous optimization perspectives.
- Walking in the Shadow: A New Perspective on Descent Directions for Constrained Minimization with Mortagy, Pokutta, NeurIPS 2020, (major rev) Mathematics of Operations Research.
- Electrical Flows over Spanning Trees with Khodabhaksh, Mortagy, Nikolova Mathematical Programming B, 2022
- Reusing Combinatorial Structure: Faster Iterative Projections over Submodular Base Polytopes with Moondra, Mortagy NeurIPS 2021
- Limited Memory Kelley’s Method Converges for Composite Convex and Submodular Objectives with Udell, Zhou NeurIPS 2018 (spotlight)
- Newton’s Method for Parametric Submodular Function Minimization with Michel Goemans, Patrick Jaillet, IPCO 2017
- Combinatorial Structure in Online and Convex Optimization, PhD Thesis, MIT 2017
- Solving Combinatorial Games using Products, Projections and Lexicographically Optimal Bases with Goemans, Jaillet NeurIPS Workshop on Optimization for ML, 2016
(b) Data-driven Optimization and AI: If we have solved an optimization problem already, then solving this on a perturbed dataset, or a related “close-by” optimization should be easier. Most first-order methods solve as a black-box (e.g., linear optimizations in Frank-Wolfe variants, projections in mirror descent variants) perturbations of the same problem, during the process of the overarching optimization. We have developed techniques to reuse combinatorial information (e.g., tight inequalities for submodular polytopes) from previous solves to exploit in the current iterations, resulting in a 2-3 orders of magnitude improvement in the running time. We are critically exploiting submodularity and combinatorial structure in such problems. This direction further lends well to augmented ML algorithms, with provable structure from previous resolves. Can optimization algorithms be speed up using AI, and can AI be speeded up using optimization subroutines? With growing scale of applications that span various constrained decision sets, there is a massive need for the two areas to work collaboratively. We are interested in exploring connections ranging from learning which algorithm works best when to understanding how AI subroutines can be used to guide optimization solvers faster.
- TACOS: Topology-Aware Collective Algorithm Synthesizer for Distributed Machine Learning with Won, Elavazhagan, Srinivasan, Krishna, MICRO 2024
- Reusing Combinatorial Structure: Faster Iterative Projections over Submodular Base Polytopes with Moondra, Mortagy, NeurIPS 2021
- Computational Comparison of Metaheuristics with Silberholz, Golden, Wang, Handbook of Metaheuristics, Springer, 2019
- What works best when? A Framework for Systematic Heuristic Evaluation with Silberholz, Dunning, INFORMS Journal on Computing, 2018
(c) Approximation Algorithms: We are interested in pushing the boundaries of provable approximations for various combinatorial problems, often motivated by practice. We have developed new approximations for the network reconfiguration problem (from power systems) using kernel-based alpha-point rounding, minimum linear ordering problems, traveling salesman problem, districting, electrical flows over networks, scheduling, ordered set cover, all-norm TSP, facility location, k-clustering, to name a few.
- Approximation Algorithms for Fair Portfolio of Solutions in Combinatorial Optimization – with Moondra, Singh, SODA 2025, arxiv.
- Which Lp norm is the fairest? Approximations for fair facility location across all “p” – with Moondra, Singh. EC 2023, arxiv.
- Hardness and Approximation of Submodular Minimum Linear Ordering Problems, with Farhadi, Sun, Tetali, Wigal Mathematical Programming 2023
- Electrical Flows over Spanning Trees with Khodabhaksh, Mortagy, Nikolova, Mathematical Programming B, 2022
- A 4/3 approximation for TSP on cubic 3-edge-connected graph with Agarwal, Garg, Operations Research Letters, 2018
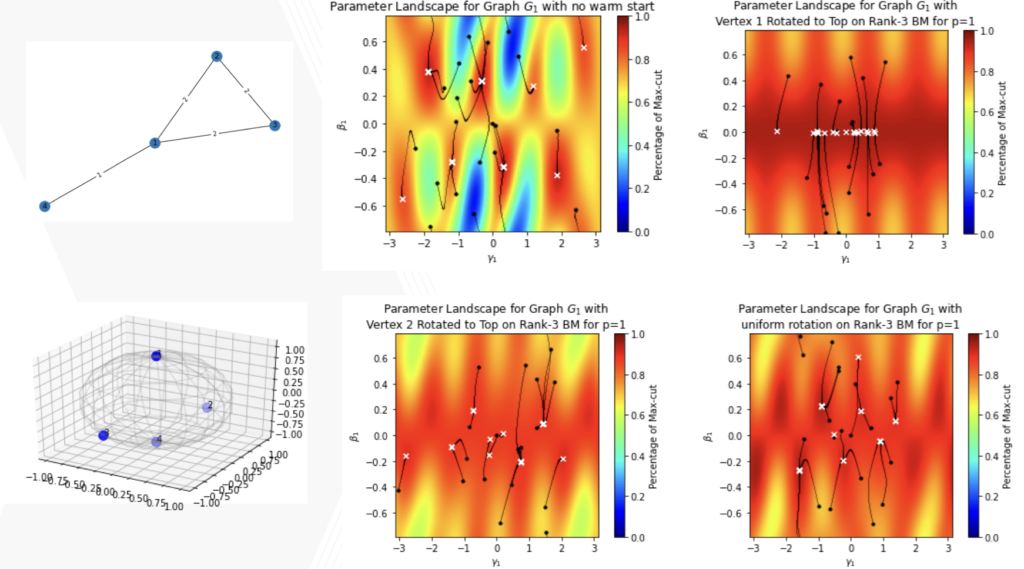
(d) Quantum Optimization: With the growing computational demands of our era, we are looking into new primitives in optimization. With support from a $9.2M DARPA grant for delving into hybrid classical-quantum methods, we are one of the first research groups in the world to bring the concept of warm-starts in quantum optimization. We are currently exploring other classical techniques that can be used to speed up hybrid quantum algorithms, such as sparsification of problem instances, decomposition, warm-starts for other combinatorial problems, incorporation of constraints, etc.
- Promise of Graph Sparsification and Decomposition for Noise Reduction in QAOA: Analysis for Trapped-Ion Compilations – with Moondra, Mohler, Lotshaw (under revision) Quantum 2025
- Strategies for running the QAOA at hundreds of qubits – with Augustino, Cain, Farhi, Gutmann, Ranard, Tang and Van Kirk (arxiv)
- Quantum Optimization: Potential, Challenges, and the Path Forward – with 40+ authors, Nature Reviews Physics 2024
- Classically-inspired Mixers for QAOA Beat Goemans-Williamson’s Max-Cut at Low Circuit Depths, with Tate, Moondra, Gard, Mohler Quantum 2023
- Generating Target Graph Couplings for QAOA from Native Quantum Hardware Couplings with Rajakumar, Moondra and Herold, Physical Review A, 2022
- Bridging Classical and Quantum using SDP initialized warm-starts for QAOA with Tate, Farhadi, Herold and Mohler ACM Transactions of Quantum Computing, 2022



Leave a Reply